Wednesday, April 8, 2015
Friday, March 27, 2015
Saturday, March 14, 2015
OpenBR + OpenCV + Qt with CMake
CMake is cross-platform free and open-source software for managing the build process of software using a compiler-independent method. It is designed to support directory hierarchies and applications that depend on multiple libraries.
OpenCV, OpenBR is popular computer vision libraries. First mainly aimed at real-time computer vision(general purposes), second mainly aimed at face detection and recognition.
OpenBR is highly dependent on Qt.
Example will consists from face detection problem. Main.cpp, CMakeLists and bash script to run all this stuff.
${PROJECT_DIR}/src/main.cpp:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 | #include <iostream> #include <QString> #include <iostream> #include <openbr/openbr_plugin.h> #include <opencv2/objdetect/objdetect.hpp> #include <opencv2/highgui/highgui.hpp> #include <opencv2/imgproc/imgproc.hpp> #include <opencv2/opencv.hpp> int main( int argc, char* argv[] ) { br::Context::initialize(argc, argv); br::Globals->quiet=true; //don't print output br::Globals->enrollAll = true; //enable to detect multiple faces QSharedPointer<br::Transform> detectionTransform = br::Transform::fromAlgorithm( "Open+Cascade(FrontalFace)+Expand" "+ASEFEyes+Draw[distribute=false]" ); cv::VideoCapture capture; capture.open(0); capture.set(CV_CAP_PROP_FRAME_WIDTH, 640); capture.set(CV_CAP_PROP_FRAME_HEIGHT, 480); if (!capture.isOpened()) { std::cerr << "---(!)Error opening video capture\n"; exit(1); } int counter = 0; time_t start, end; double fps; time(&start); cv::Mat frame, final; while(capture.read(frame)) { time(&end); fps = round(++counter / difftime(end,start)); std::stringstream ss; ss << fps; // Openbr magic br::Template query(frame); br::Globals->enrollAll = true; query >> *detectionTransform; cv::Mat detectionResult = query.m().clone(); if (detectionResult.rows != 0) { final = detectionResult; } else { final = frame; } //add Fps to frame putText(final, "FPS: " + ss.str(), cv::Point(10, 30), cv::FONT_HERSHEY_PLAIN, 2, cv::Scalar::all(255), 2, 3); imshow("Test", final); int c = cv::waitKey(5); if ((c == 'c') || (c == 'q') || (c == 27)) { break; } } br::Context::finalize(); } |
${PROJECT_DIR}/src/CMakeLists.txt:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | cmake_minimum_required(VERSION 2.8.11) project(MainTest) set(CMAKE_AUTOMOC ON) set(CMAKE_INCLUDE_CURRENT_DIR ON) find_package(OpenCV REQUIRED) find_package(OpenBR REQUIRED) link_directories(/usr/lib/) find_package(Qt5 5.4.0 REQUIRED Core Gui Xml ) include_directories(${Qt5Widgets_INCLUDE_DIRS} ${Qt5Core_INCLUDE_DIRS} ${Qt5Gui_INCLUDE_DIRS}) add_executable(MainTest main.cpp) target_link_libraries(MainTest ${OpenCV_LIBS} ${OPENBR_LIBS} Qt5::Core) |
${PROJECT_DIR}/start.sh:
1 2 3 4 5 6 | rm -rf build mkdir build cd build cmake -DCMAKE_PREFIX_PATH=/usr/local/Cellar/qt5/5.4.0 ../src make ./MainTest |
Few Notes:
1. You should change DCMAKE_PREFIX_PATH to your Qt path.
2. Change Qt Version in CMakeLists.txt if you have 5.1.1 as example.
Friday, March 13, 2015
Multi Agent Games for Pacman
Post will consists from implementing Minimax, Alfa-Beta pruning and Expectimax algorithms.
Minimax
This algorithm mainly for zero-sum games. It helps to make decisions for minimising the possible loss for a worst case scenario.
You can read more about zero-sum games http://en.wikipedia.org/wiki/Zero-sum_game and about minimax algorithm http://en.wikipedia.org/wiki/Minimax.
Complex property of minimax algorithm is deep level. How deep we should see the nearest future?
We need to implement maxvalue and minvalue functions. Maxvalue function is used by our Pacman. Minvalue function is used by ghosts.
Implementation will consist from four simple functions.
- Maxvalue ~ for computing the best direction for Pacman.
- Minvalue ~ for computing the worst case actions for ghosts.
- Value ~ for generalisation of maxvalue and minvalue.
- GetAction ~ function which is called for getting the best action for current position of Pacman (with deep level parameter).
Maxvalue function
def maxvalue(self ,state, agentIndex, currentdepth): v = (float("-inf"), "Stop") for action in state.getLegalActions(agentIndex): v = max([v, (self.value(state.generateSuccessor(agentIndex, action), \ (currentdepth+1) % self.number_of_agents, currentdepth+1), action)], key=lambda item:item[0]) return v
Minvalue function
def minvalue(self, state, agentIndex, currentdepth): v = (float("inf"), "Stop") for action in state.getLegalActions(agentIndex): v = min([v, (self.value(state.generateSuccessor(agentIndex, action), \ (currentdepth+1) % self.number_of_agents, currentdepth+1), action)], key=lambda item:item[0]) return v
Value function
def value(self, state, agentIndex, currentdepth): if state.isLose() or state.isWin() or currentdepth >= self.depth*self.number_of_agents: return self.evaluationFunction(state) if (agentIndex == 0): return self.maxvalue(state, agentIndex, currentdepth)[0] else: return self.minvalue(state, agentIndex, currentdepth)[0]
GetAction function
def getAction(self, gameState): self.number_of_agents = gameState.getNumAgents() path2 = self.maxvalue(gameState,0,0) return path2[1]
Alpha-Beta Prunning
Maxvalue function
def maxvalue(self ,state, agentIndex, currentdepth, alpha, beta): v = (float("-inf"), "Stop") for action in state.getLegalActions(agentIndex): v = max([v, (self.value(state.generateSuccessor(agentIndex, action), (currentdepth+1) % self.number_of_agents, currentdepth+1, alpha, beta), action)], key=lambda item:item[0]) if v[0] > beta: return v alpha = max(alpha, v[0]) return v
Minvalue function
def minvalue(self, state, agentIndex, currentdepth, alpha, beta): v = (float("inf"), "Stop") for action in state.getLegalActions(agentIndex): v = min([v, (self.value(state.generateSuccessor(agentIndex, action), (currentdepth+1) % self.number_of_agents, currentdepth+1, alpha, beta), action)], key=lambda item:item[0]) if v[0] < alpha: return v beta = min(beta, v[0]) return v
Value function
def value(self, state, agentIndex, currentdepth, alpha, beta): if state.isLose() or state.isWin() or currentdepth >= self.depth*self.number_of_agents: return self.evaluationFunction(state) if (agentIndex == 0): return self.maxvalue(state, agentIndex, currentdepth, alpha, beta)[0] else: return self.minvalue(state, agentIndex, currentdepth, alpha, beta)[0]
GetAction function
def getAction(self, gameState): self.number_of_agents = gameState.getNumAgents() alpha = float("-inf") beta = float("inf") path2 = self.maxvalue(gameState,0,0,alpha,beta) return path2[1]
Expectimax
Expected value function
def expectedvalue(self, state, agentIndex, currentdepth): v = [0.0] for action in state.getLegalActions(agentIndex): v.append(self.value(state.generateSuccessor(agentIndex, action), (currentdepth+1) % self.number_of_agents, currentdepth+1)) return sum(v)/(len(v)-1)
Saturday, February 28, 2015
Comparing Search Algorithms for Pacman Game
- Depth First Search
- Breadth First Search
- Uniform Cost Search
- A-start Search with consistent heuristic
- Path total cost = 210
- Time = 0.0 seconds
- Nodes Expanded = 390
- Path total cost = 130
- Time = 0.0 seconds
- Nodes Expanded = 146
- Path total cost = 210
- Time = 0.0 seconds
- Nodes Expanded = 620
- Path total cost = 68
- Time = 0.0 seconds
- Nodes Expanded = 269
- Path total cost = 210
- Time = 0.0 seconds
- Nodes Expanded = 620
- Path total cost = 68
- Time = 0.0 seconds
- Nodes Expanded = 269
- Path total cost = 210
- Time = 0.0 seconds
- Nodes expanded = 549
Tuesday, February 17, 2015
Sentence Clusterization
Load data files
Data is from ics.uci.edu/ml
Opinion Reviews.
data.battery <- read.table("data/battery-life_amazon_kindle.txt.data", sep = "\n", stringsAsFactors = FALSE, strip.white = TRUE) data.windows7 <- read.table("data/features_windows7.txt.data", sep = "\n", stringsAsFactors = FALSE, strip.white = TRUE)
## Warning in scan(file, what, nmax, sep, dec, quote, skip, nlines, ## na.strings, : EOF within quoted string
data.keyboard <- read.table("data/keyboard_netbook_1005ha.txt.data", sep="\n", stringsAsFactors = FALSE, strip.white = TRUE) data.honda <- read.table("data/performance_honda_accord_2008.txt.data", sep = "\n", stringsAsFactors = FALSE, strip.white = TRUE) data.ipod <- read.table("data/video_ipod_nano_8gb.txt.data", sep = "\n", stringsAsFactors = FALSE, strip.white = TRUE)
library(gdata) sentences <- c() for (i in 1:dim(data.battery)[1]) {sentences <- c(sentences, trim(data.battery[i,1]))} for (i in 1:dim(data.windows7)[1]){sentences <- c(sentences, trim(data.windows7[i,1]))} for (i in 1:dim(data.keyboard)[1]){sentences <- c(sentences, trim(data.keyboard[i,1]))} for (i in 1:dim(data.honda)[1]) {sentences <- c(sentences, trim(data.honda[i,1]))} for (i in 1:dim(data.ipod)[1]) {sentences <- c(sentences, trim(data.ipod[i,1]))}
sentences[1:10]
## [1] "After I plugged it in to my USB hub on my computer to charge the battery the charging cord design is very clever !" ## [2] "After you have paged tru a 500, page book one, page, at, a, time to get from Chapter 2 to Chapter 15, see how excited you are about a low battery and all the time it took to get there !" ## [3] "NO USER REPLACEABLE BATTERY, , Unless you buy the extended warranty for $65 ." ## [4] "After 1 year you pay $80 plus shipping to send the device to Amazon and have the Kindle REPLACED, not the battery changed out ." ## [5] "The fact that Kindle 2 has no SD card capability and the battery is not user, serviceable is not an issue with me ." ## [6] "Things like the buttons that made it easy to accidentally turn pages the separate cursor on the side that could only select lines and was sometimes hard to see the occasionally awkward menus the case which practically forced you to remove it to use it and sometimes pulled the battery door off ." ## [7] "The issue with the battery door opening is thus solved, but Amazon went further, eliminating the door altogether and wrapping the back with sleek stainless steel ." ## [8] "Frankly, I never used either the card slot or changed the battery on my Kindle 1 but I liked that they were there and I miss them on the Kindle 2, even though, I have to admit, I dont actually need them .\n Its also easy to charge the Kindle in the car if you have a battery charger with a USB port ." ## [9] "You cant carry an extra battery , though with the extended battery life and extra charging options its almost a non, issue , and you cant replace the battery because of the iPod, like fixed backing .\n For one thing, theres no charge except battery power no pun intended !" ## [10] "Before purchasing, I was obsessed with the reviews and predictions I found online and reading about some of the critiques such as the thick border, the lack of touchscreen, lack of battery SD slot, lack of a back light, awkward difficult keyboard layout, minimally faster page flipping, and the super, high price ."
library(Matrix) library(gamlr) library(parallel) library(distrom) library(textir) library(NLP) library(tm) library(SnowballC)
corpus <- VCorpus(VectorSource(sentences)) corpus <- tm_map(corpus, content_transformer(function(x) iconv(x, to='UTF-8-MAC', sub='byte')), mc.cores=1) corpus <- tm_map(corpus, content_transformer(removePunctuation), lazy = TRUE) my.stopwords <- c(stopwords('english'), "the", "great", "use") corpus <- tm_map(corpus, removeWords, c(stopwords('english'), "the", "great")) corpus <- tm_map(corpus, removeNumbers) corpus <- Corpus(VectorSource(corpus)) dtm <- DocumentTermMatrix(corpus, control=list(minWordLength=4, minDocFreq=4)) dtm
## <<DocumentTermMatrix (documents: 245, terms: 1492)>> ## Non-/sparse entries: 4171/361369 ## Sparsity : 99% ## Maximal term length: 14 ## Weighting : term frequency (tf)
df <- as.data.frame(inspect(dtm)) m <- t(as.matrix(df)) d <- dist(m)
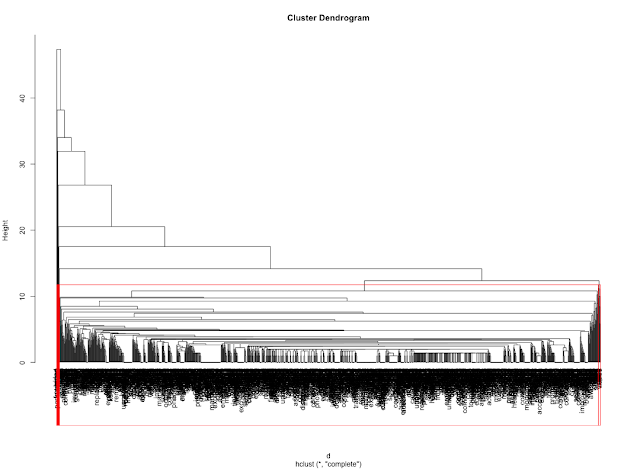
hr <- hclust(d, method = "complete", members=NULL) plot(hr)
plot(hr, hang = -1) rect.hclust(hr, 10)
set.seed(1235) df <- df[,!colnames(df)%in%my.stopwords] cl = kmeans(df, centers = 10, nstart = 50, iter.max = 100) res = cl$centers discr = apply(cl$centers, 2, sd) r = sort(discr, decreasing = TRUE, index = TRUE)$ix[1:10] print(r)
## [1] 902 439 1372 643 105 169 180 1418 681 990
barplot(cl$centers[,r],beside=TRUE, col=rainbow(10))
Let's fix this problem with k-means stability.
for(i in 1:50){ cl = kmeans(df, centers = 10, nstart = 50, iter.max = 100) tt = cl$centers for(j in 1:length(tt)) { tt[i] = tt[i] + cl$centers[sort(abs(tt - cl$centers), i=T)$ix[1]] tt = tt/2 } } discr = apply(cl$centers, 2, sd) r = sort(discr, decreasing = TRUE, index = TRUE)$ix[1:10] barplot(cl$centers[,r],beside=TRUE, col=rainbow(10))
Orange cluster interested in ['camera', 'video', 'ipod']
Cyan cluster interested in ['performance', 'car']
Light green cluster interested in ['camera', 'video'], but less than orange cluster
Dark Blue cluster interested in ['features', 'windows']
Blue cluster intereted in ['battery', 'keyboard', 'life']
Purple cluster interested in ['battery', 'life']
Yellow cluster interestedn in ['keyboard']
This 100% unsupervised approach to cluster this type of data. And we obtain good segmentation of our sentences into topics. It can be improved a lot using stemming for large datasets. This approach can help you to understand your data from another side. Welcome!sessionInfo()
## R version 3.1.2 (2014-10-31) ## Platform: x86_64-apple-darwin13.4.0 (64-bit) ## ## locale: ## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8 ## ## attached base packages: ## [1] parallel stats graphics grDevices utils datasets methods ## [8] base ## ## other attached packages: ## [1] SnowballC_0.5.1 tm_0.6 NLP_0.1-6 textir_2.0-2 ## [5] distrom_0.3-1 gamlr_1.12-1 Matrix_1.1-5 gdata_2.13.3 ## [9] knitr_1.9 ## ## loaded via a namespace (and not attached): ## [1] evaluate_0.5.5 formatR_1.0 grid_3.1.2 gtools_3.4.1 ## [5] highr_0.4 lattice_0.20-29 slam_0.1-32 stringr_0.6.2 ## [9] tools_3.1.2
Thursday, February 12, 2015
Analyzing the NYC Subway Dataset
Section 0. Preparation¶
import matplotlib
%matplotlib inline
import matplotlib.dates as mdates
#%matplotlib osx
import pandas
import numpy
from ggplot import *
import statsmodels.api as sm
import statsmodels
import scipy
import matplotlib.pyplot as plt
import math
import seaborn as sns
from datetime import datetime
df = pandas.read_csv('turnstile_data_master_with_weather.csv')
non_rain = df['ENTRIESn_hourly'][df['rain'] == 0]
rain = df['ENTRIESn_hourly'][df['rain'] == 1]
Before doing anything I want to have a look at data.
df.describe()
| Unnamed: 0 | Hour | ENTRIESn_hourly | EXITSn_hourly | maxpressurei | maxdewpti | mindewpti | minpressurei | meandewpti | meanpressurei | fog | rain | meanwindspdi | mintempi | meantempi | maxtempi | precipi | thunder | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951.000000 | 131951 |
| mean | 65975.000000 | 10.896158 | 1095.348478 | 886.890838 | 30.031894 | 57.241302 | 48.259013 | 29.892714 | 52.703526 | 29.965077 | 0.167100 | 0.334245 | 5.543065 | 56.169775 | 64.269729 | 71.769968 | 0.172276 | 0 |
| std | 38091.117022 | 6.892084 | 2337.015421 | 2008.604886 | 0.125689 | 8.770891 | 11.305312 | 0.146384 | 9.943590 | 0.130461 | 0.373066 | 0.471728 | 1.982441 | 6.338875 | 6.568289 | 7.627218 | 0.429005 | 0 |
| min | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 29.740000 | 39.000000 | 22.000000 | 29.540000 | 31.000000 | 29.640000 | 0.000000 | 0.000000 | 1.000000 | 46.000000 | 55.000000 | 58.000000 | 0.000000 | 0 |
| 25% | 32987.500000 | 5.000000 | 39.000000 | 32.000000 | 29.960000 | 50.000000 | 38.000000 | 29.840000 | 45.000000 | 29.910000 | 0.000000 | 0.000000 | 5.000000 | 52.000000 | 60.000000 | 65.000000 | 0.000000 | 0 |
| 50% | 65975.000000 | 12.000000 | 279.000000 | 232.000000 | 30.030000 | 57.000000 | 51.000000 | 29.910000 | 54.000000 | 29.960000 | 0.000000 | 0.000000 | 5.000000 | 54.000000 | 63.000000 | 71.000000 | 0.000000 | 0 |
| 75% | 98962.500000 | 17.000000 | 1109.000000 | 847.000000 | 30.100000 | 64.000000 | 55.000000 | 29.970000 | 60.000000 | 30.050000 | 0.000000 | 1.000000 | 6.000000 | 60.000000 | 68.000000 | 78.000000 | 0.100000 | 0 |
| max | 131950.000000 | 23.000000 | 51839.000000 | 45249.000000 | 30.310000 | 70.000000 | 66.000000 | 30.230000 | 68.000000 | 30.270000 | 1.000000 | 1.000000 | 12.000000 | 70.000000 | 78.000000 | 86.000000 | 2.180000 | 0 |
Section 1. Statistical Test¶
The first question which I asked myself was: Is there any significant difference between number of people entering subway in rainy and non rainy days. As shown below, data for this particular question isn't normally distributed. So it's suitable to use non-parametric test. I'm going to use Mann–Whitney U test. Null hypothesis for our two-sided test will be P(x>y)=0.5, where x - subway crowd in rainy days, y - subway crowd in non rainy days. At first let's check our assumptions about non-Gaussian data using Shapiro-Wilk test:
scipy.stats.shapiro(rain)
(0.4715914726257324, 0.0)
scipy.stats.shapiro(non_rain)
(0.47661787271499634, 0.0)
Personaly, I'm very sceptic and always want to confirm results using another approach. For second normality test I'll use scipy.stats.mstats.normaltest based on D'Agostino and Pearson's test (more information you can find in docs.scipy.org. The method returns p-value for 2-sided chi-quared probability for the hypothesis test.
scipy.stats.mstats.normaltest(rain)
(49379.024966302793, 0.0)
scipy.stats.mstats.normaltest(non_rain)
(96614.17551121171, 0.0)
As we can see from Shapiro-Wilk and D'Agostino|Pearson test data is definitely non normal distributed due to extremely low p-value. Now let's calculate statistics and p-value for Mann Whitney U test (wikipedia.org) and it's python implementation scipy.stats:
t, p_value = scipy.stats.mannwhitneyu(rain, non_rain)
2 * p_value
0.049999825586979442
We multiplied p-value by two in Mann Whitney U test, because scipy returns p-value for one-sided test. P-value is less than 0.05 - our significant level, so we should reject the null hypothesis that the distributions being compared are identical. Let examine this data more and look at means and medians.
"rain mean = {0}, non-rain mean = {1}".format(numpy.mean(rain), numpy.mean(non_rain))
'rain mean = 1105.44637675, non-rain mean = 1090.27878015'
"rain median = {0}, non-rain median = {1}".format(numpy.median(rain), numpy.median(non_rain))
'rain median = 282.0, non-rain median = 278.0'
So it seems that statistical tests are right. In my opinion in shiny days people can walk on the street to work/university. But in rany days it's quite not comfortable, so maybe here is one of the differences. Also I should notice that I used significance level 5%.
Section 2. Linear Regression¶
In my investigation of given dataset I was trying to predict how many people will enter subway using different predictors. I've used gradient descent and ols methods for this problem. I want to show prediction using ols method. Our response variable will be 'ENTRIESn_hourly'. Our predictiors will be 'EXITSn_hourly', 'rain', 'fog'. Let's notice that rain and fog is our dummy variables. I decided to use fog and rain because I thought that when it is very foggy or rainy outside people might decide to use the subway more often. Also I decided to use hour variable because it increases R-squared value and maxtempi & meandewpti for their high variance. 'EXITSn_hourly' present in model due to my believings that number of entries in subway is extremely correlated with number of exits.
y = df['ENTRIESn_hourly']
x = df[['EXITSn_hourly' ,'rain', 'fog', 'meantempi', 'Hour','meandewpti']]
x = sm.add_constant(x)
model = sm.OLS(y,x)
results = model.fit()
results.summary()
| Dep. Variable: | ENTRIESn_hourly | R-squared: | 0.557 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.557 |
| Method: | Least Squares | F-statistic: | 2.770e+04 |
| Date: | Thu, 29 Jan 2015 | Prob (F-statistic): | 0.00 |
| Time: | 19:18:45 | Log-Likelihood: | -1.1569e+06 |
| No. Observations: | 131951 | AIC: | 2.314e+06 |
| Df Residuals: | 131944 | BIC: | 2.314e+06 |
| Df Model: | 6 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [95.0% Conf. Int.] | |
|---|---|---|---|---|---|
| const | 324.5246 | 46.355 | 7.001 | 0.000 | 233.670 415.379 |
| EXITSn_hourly | 0.8549 | 0.002 | 395.953 | 0.000 | 0.851 0.859 |
| rain | -8.7396 | 12.559 | -0.696 | 0.486 | -33.355 15.875 |
| fog | 44.6593 | 13.107 | 3.407 | 0.001 | 18.970 70.348 |
| meantempi | -2.6079 | 1.020 | -2.556 | 0.011 | -4.608 -0.608 |
| Hour | 19.7716 | 0.629 | 31.430 | 0.000 | 18.539 21.005 |
| meandewpti | -0.7543 | 0.728 | -1.036 | 0.300 | -2.182 0.673 |
| Omnibus: | 109690.964 | Durbin-Watson: | 1.504 |
|---|---|---|---|
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 25879157.660 |
| Skew: | 3.164 | Prob(JB): | 0.00 |
| Kurtosis: | 71.316 | Cond. No. | 2.39e+04 |
From our summary model we can see that rain variable is significant for our prediction due to 95% confidence interval contain 0 so we can surely say that rain variable is not so important in current variables configuration. In summary of our model we can observe mathematical expectation of coefficients of dummy or non-dummy variables, standard deviation, confidence interval and more different useful statistics.
Coefficient of determination of our model is equal to 0.558. I want to remember that coefficient of determination has the following meaning - this is the percentage of variance that is explained by our model. We can see that our R-squared is too low to produce accurate predictions.
Section 3. Visualization¶
Let's plot our ols prediction results. Let y-axis be 'ENTRIESn_hourly' and x-axis be 'EXITSn_hourly'. Plotting will be done using matplotlib.
fig, ax = plt.subplots()
statsmodels.graphics.regressionplots.plot_fit(results, 'EXITSn_hourly', ax=ax)
ax.set_ylabel("ENTRIESn_hourly")
ax.set_xlabel("EXITSn_hourly")
ax.set_title("Linear Regression")
plt.axis([0, 60000, 0, 60000])
fig1 = matplotlib.pyplot.gcf()
fig1.set_size_inches(10.5,10.5)
plt.show()
As we can see from plot, we haven't got good model to predict ENTRIESn_hourly on each subway station. Let's create visualization which contains two histograms: one of ENTRIESn_hourly for rainy days and one of ENTRIESn_hourly for non-rainy days. For this visualization i've used ggplot.
df_t = df.copy(True)
df_t['rain'][df_t['rain'] == 0] = 'no rain'
df_t['rain'][df_t['rain'] == 1] = 'rain'
df_t.describe()
ggplot(df_t, aes(x = 'ENTRIESn_hourly')) + geom_histogram(binwidth = 200) + facet_wrap('rain') + xlim(0,5000) +\
ggtitle("Hitograms of ENTRIESn_hourly by rain") + ylab('Frequency')
Let's add more plots and look at subway daily entries/exits with time.
df1 = df[['ENTRIESn_hourly', 'DATEn']].groupby('DATEn').sum()
df2 = df[['EXITSn_hourly', 'DATEn']].groupby('DATEn').sum()
df1.index.name = 'Date'
df1.reset_index(inplace=True)
df2.index.name = 'Date'
df2.reset_index(inplace=True)
df1.columns = ['Date', 'NumberOfPeople']
df2.columns = ['Date', 'NumberOfPeople']
df1['type'] = 'ENTRIESn_hourly'
df2['type'] = 'EXITSn_hourly'
total = pandas.concat([df1,df2])
total['Date'] = pandas.to_datetime(total['Date'])
start = min(total['Date'])
end = max(total['Date'])
gg = ggplot(total, aes(x='Date', y='NumberOfPeople', color = 'type')) + geom_point() + geom_line() +\
ggtitle("Daily entries and exits") + ylim(0, 6500000)
print gg
Surprisingly, but I my thoughts are very different from this plot. I was thinking that summary number of Entries & Exits in subway should be near same value, but from plot we can see big difference between this two variables. Difference is explained by the reason that some subway station in NY doesn't have turnstile on exits. Also it's very common that less people use subway in weekends. Notes: unfortunately ggplot can't natively scale date axis - https://github.com/yhat/ggplot/issues/312. There are some bugs with limits.
The last one - let's create histogram plot of ENTRIESn_hourly depending on weather i.e. fog and rain As in class we will create fog-rain variable at first.
def format_key(fog, rain):
return '{}fog-{}rain'.format(
'' if fog else 'no',
'' if rain else 'no')
fograin = []
for index, row in df.iterrows():
fograin.append(format_key(row['fog'], row['rain']))
df['fograin'] = pandas.Series(fograin)
ggplot(df, aes(x='ENTRIESn_hourly', fill='fograin', color='fograin')) + \
geom_histogram(alpha=0.6, binwidth = 200) + xlim(0,5000) + \
xlab("Number of people") + ylab("Frequency") + ggtitle("Histogram of Entries hourly by type of weather")
From plot we can observe that mode of number of peoples in subway stay near the same. Also we can notice that our data is highly right skewed distributed.
Section 3.5. Prediction of future daily entries using linear regression.¶
At first I should notice that I can't use EXITSn_hourly for future predictions, because i simply don't know this values. So i can use only weather values which i can obtain from meteorological station. In section 3 i notice that data is seems to very seasonal, so it might be a right way to add to linear regression some features to catch seasonal (daily) changings. So i'm going to add seasonal pattern using Fourier terms.
#Read again data
df = pandas.read_csv('turnstile_data_master_with_weather.csv')
#define season in seconds (1 week)
season = 7 * 24 * 60 * 60
df1 = df[['ENTRIESn_hourly', 'DATEn']].groupby('DATEn').sum()
df1.index.name = 'Date'
df1.reset_index(inplace=True)
df1.columns = ['Date', 'NumberOfPeople']
df2 = df[['meanwindspdi', 'mintempi', 'meantempi', 'maxtempi','maxpressurei', 'maxdewpti', 'mindewpti', 'minpressurei', 'meandewpti', 'meanpressurei', 'DATEn']].groupby('DATEn').mean()
df2.reset_index(inplace=True)
##concat df1 and df2
main = pandas.concat([df1,df2], 1)
main = main.drop('DATEn', 1)
main['Date'] = pandas.to_datetime(main['Date'])
main['UnixTime'] = main['Date'].astype(numpy.int64) // 10**9
#function to add fourier terms to data frame, n - number of terms
def add(df, n, col_time_name):
for i in range(1,n+1):
col_sin_name = "sin" + str(i)
col_cos_name = "cos" + str(i)
sin = lambda x: math.sin(2*math.pi*i*x/season)
cos = lambda x: math.cos(2*math.pi*i*x/season)
df[col_sin_name] = df[col_time_name].apply(sin)
df[col_cos_name] = df[col_time_name].apply(cos)
return df
main = add(main, 2, 'UnixTime')
cols = list(main.columns.values)
cols_x = [x for x in cols if x not in ['NumberOfPeople', 'Date', 'UnixTime']]
y = main['NumberOfPeople']
x = main[cols_x]
x = sm.add_constant(x)
model = sm.OLS(y,x)
results = model.fit()
results.summary()
| Dep. Variable: | NumberOfPeople | R-squared: | 0.951 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.905 |
| Method: | Least Squares | F-statistic: | 20.64 |
| Date: | Thu, 29 Jan 2015 | Prob (F-statistic): | 2.77e-07 |
| Time: | 19:19:17 | Log-Likelihood: | -420.42 |
| No. Observations: | 30 | AIC: | 870.8 |
| Df Residuals: | 15 | BIC: | 891.9 |
| Df Model: | 14 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [95.0% Conf. Int.] | |
|---|---|---|---|---|---|
| const | -1.54e+07 | 2.48e+07 | -0.622 | 0.543 | -6.82e+07 3.74e+07 |
| meanwindspdi | -8130.3111 | 5.44e+04 | -0.149 | 0.883 | -1.24e+05 1.08e+05 |
| mintempi | -2.794e+05 | 1.94e+05 | -1.443 | 0.169 | -6.92e+05 1.33e+05 |
| meantempi | 6.312e+05 | 3.57e+05 | 1.766 | 0.098 | -1.31e+05 1.39e+06 |
| maxtempi | -3.549e+05 | 1.76e+05 | -2.012 | 0.063 | -7.31e+05 2.12e+04 |
| maxpressurei | 1.054e+07 | 4.11e+06 | 2.563 | 0.022 | 1.77e+06 1.93e+07 |
| maxdewpti | 1.342e+05 | 7.44e+04 | 1.804 | 0.091 | -2.44e+04 2.93e+05 |
| mindewpti | 7.91e+04 | 7.49e+04 | 1.057 | 0.307 | -8.05e+04 2.39e+05 |
| minpressurei | -1.229e+06 | 2.63e+06 | -0.467 | 0.647 | -6.84e+06 4.38e+06 |
| meandewpti | -2.253e+05 | 1.39e+05 | -1.618 | 0.126 | -5.22e+05 7.14e+04 |
| meanpressurei | -8.627e+06 | 4.91e+06 | -1.756 | 0.099 | -1.91e+07 1.84e+06 |
| sin1 | -9.192e+05 | 1.5e+05 | -6.119 | 0.000 | -1.24e+06 -5.99e+05 |
| cos1 | 1.529e+06 | 1.62e+05 | 9.460 | 0.000 | 1.18e+06 1.87e+06 |
| sin2 | 5.624e+05 | 1.44e+05 | 3.909 | 0.001 | 2.56e+05 8.69e+05 |
| cos2 | -1.866e+05 | 1.33e+05 | -1.406 | 0.180 | -4.7e+05 9.64e+04 |
| Omnibus: | 9.581 | Durbin-Watson: | 1.863 |
|---|---|---|---|
| Prob(Omnibus): | 0.008 | Jarque-Bera (JB): | 8.179 |
| Skew: | -1.038 | Prob(JB): | 0.0167 |
| Kurtosis: | 4.494 | Cond. No. | 5.04e+04 |
Let's create visualization.
pr = pandas.Series(results.predict())
#Construct data with fitted values and real values
final1 = pandas.DataFrame(dict(values = pr, date = main['Date']))
final2 = pandas.DataFrame(dict(values = main['NumberOfPeople'], date = main['Date']))
final1['type'] = 'fitted values'
final2['type'] = 'real values'
final = pandas.concat([final1, final2])
#crete visualization
gg = ggplot(final, aes(x='date', y='values', color = 'type')) + geom_point() + geom_line() +\
ggtitle("Fitting daily entries using Linear Regression with Fourier terms") + ylim(0, 6600000)
print gg
As we can see after adding seasonal pattern we highly increase R-squared up to 0.95 using only 4 Fourier terms.
Section 4. Conclusion¶
In this first project we partially investigate NYC Subway Dataset. I was trying to answer the following question: "Do more people ride the NYC subway when it is raining or when it is not raining?". As part of this investigation I've obtain two samples (rainy and non rainy days). I needed to check zero hypothesis that means of two samples are equal. At first i need to choose statistical test to do this task correctly. I've checked both samples on normality test. Shapiro-Wilk test rejected zero hypothesis about data normality for both samples. So I've choosen Mann-Whitney U test or Wilcoxon rank test, because it is non-parametric test (no assumptions about distributions). For our two samples Mann-Whitney U test has rejected hypothesis. So looking at mean and median for rainy and not days (both greater for rainy days meandif = 15, mediandif = 4), using results of statistical test we can conclude that distribution of the number of entries statistically different between rainy and non rainy days with significance level 5%. Linear Regression using only features from dataset gave not bad and no good. Results can be as start point, but model is bad for accurate predictions. There is still need more investigation to make right decision, but anyway I believe in non-parametric approach more. I've build ols model with not so good r-square equals to 0.557. But it can be only initial solution before more deeper diving in this dataset. But there are some issues with Linear Regression if we plan to use it for prediction. We'll definitely exclude regressors as 'EXITSn_hourly', because we arn't able to get this values. Looking at we can see that daily entries have seasonal pattern, so I've included Fourier terms to catch this fact. I've obtained good R-squared 0.95 and this model can be used for predictions. Also i want to notice that seasonal linear regression also includes variables like daily minimal temperature, maximum temperature and etc. This values i can get from meteorological station.
Section 5. Reflection¶
I've found next potential shortcomings of dataset we use: 1. Daily entries aren't equal to daily exits. Is this a bug? Or maybe I just don't have clear understanding of EXITSn_hourly. I think that entries is how many people enter subway, exits - number of people exiting subway. I'm sure this variables should be daily equal. 2. Just one month of data. This implies low variablity of tempreture and other interesting features, so they might be not so important in May, but can be extremely useful in winter.
Some notes about application of Linear Regression to our dataset: 1. It's clear to see from figure that our data is seasonal. So we might include seasonal features to predict ENTRIESn_hourly. But classic linear regression doesn't take seasonality into account. 2. I've include seasonality pattern in Linear Regression using Fourier terms. I've obtained high R-squared equal to 0.96. Model was built withou EXITSn_hourly, so we can use it to predict future values of daily entries in NYC subway.
Last notes about statistical tests: 1. In my opinion for any test I should use at least two different approaches to calculate p-value for zero hypothesis. But actually i didn't find fully another approach of non parametric test for my task. Tests on data normality is more developed and i found a good amount of approaches for using in different situations.
P.S. All source code and ipython notebook can be found on github.
List of Resources.¶
- Scipy - Normal test. Url: http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.mstats.normaltest.html
- Wikipedia - Mann-Whitney U test. Url: http://en.wikipedia.org/wiki/Mann–Whitney_U_test
- Scipy - Mann-Whitney U test. Url: http://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.stats.mannwhitneyu.html
- StatsModels - Regression. Url: http://statsmodels.sourceforge.net/0.5.0/generated/statsmodels.regression.linear_model.OLS.html
- Date Axis Limits GGplot Issue. Url: https://github.com/yhat/ggplot/issues/312
- StatsModels - OLS. Url: http://statsmodels.sourceforge.net/devel/examples/notebooks/generated/ols.html
- Python GGplot - GGplot documentation. Url: http://ggplot.yhathq.com/docs/index.html